1. Introduction
Dynamic Programming (DP)은 MDP로 정의한 문제에서 Bellman Eq.를 푸는 방법이다. DP를 적용하기 위해서는 model의 dyamics를 정확히 알고 있어야 한다 (Model-based). 여기서 model의 dynamics를 알고 있다는 의미는 Agent가 MDP에서 state transition probability를 알고 있다는 의마와 동일하다. 엄밀하게 의미하면 DP는 RL에 속하지 않고 MDP를 푸는 기법 중 하나이지만, Model-free한 RL 문제를 해결하기 위한 알고리즘의 근간이 된다.
2. DP Algorithm
DP Algorithm은 MDP에서 State-Value Function에 대한 Bellman Eq.를 풀어서 Optimal Policy를 도출하는 알고리즘이다. DP Algorithm을 통해 MDP의 모든 state에 대하여 State-Value Function을 도출하고, 이를 통해 Optimal Policy를 도출한다. State-Value Funtion의 Bellman Eq.를 푸는 과정에서 Policy를 평가 (Policy Evaluation) 하고, Policy를 개선 (Policy Improvement) 하는 과정을 수행한다. Policy Evaluation + Policy Improvement의 과정을 합쳐서 Policy를 제어 (Policy Control) 한다고 한다. DP 알고리즘에는 크게 Policy Iteration과 Value Iteration 방법이 있다.
2-1. Policy Iteration
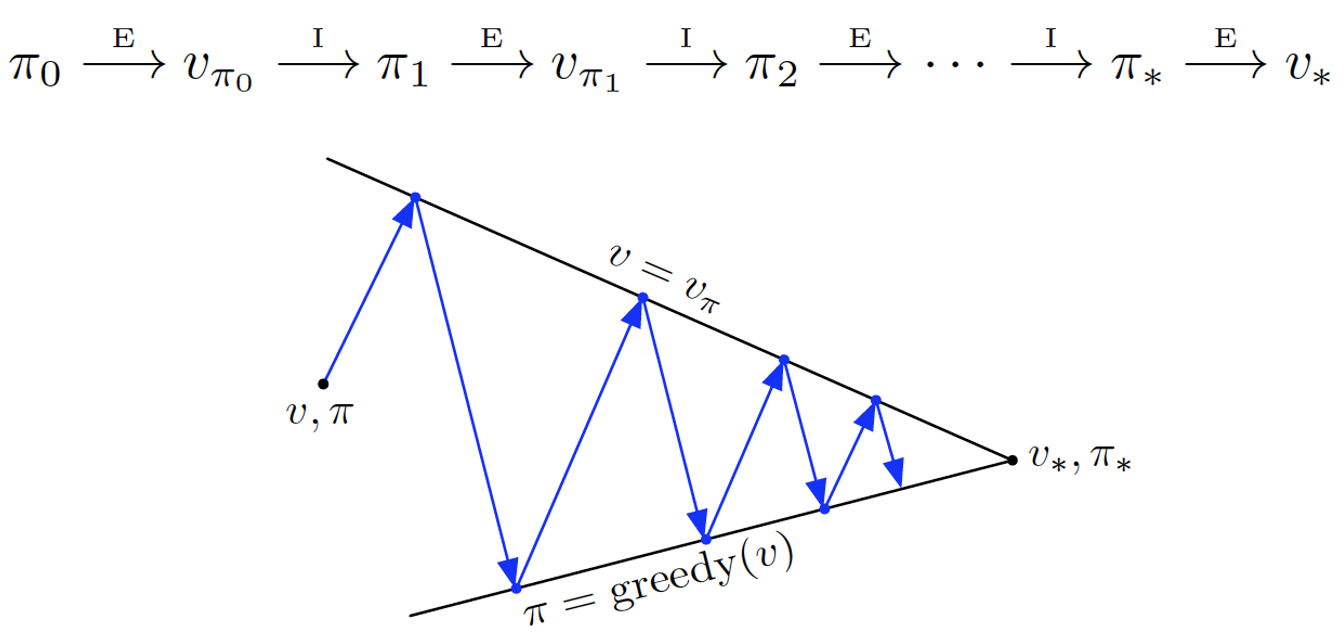
다음 그림과 같이, 임의로 초기화된 State와 Policy에 대해 Policy의 평가와 개선을 반복 수행하는 알고리즘이다.
Policy Iteration
- 2-1-1. Initialization
MDP 환경에 대해 임의의 Policy ($\pi_{0}$)로 초기화 하고, 모든 State에 대한 State-value function ($v_0(s)$)을 임의의 값으로 초기화 한다.
- 2-1-2. Policy Evaluation
DP에서는 MDP의 dynamics를 알고 있다. 따라서, 다음 수식을 통해, 현재 Policy ($\pi$) 에 대해 모든 State에 대한 State-Value Function ($v_{\pi}(s)$)을 구할 수 있다.
\[v_{k+1}(s) \leftarrow \sum_{s', r} p(s', r | s, \pi(s)) \left\{ r + \gamma v_k(s') \right\}\]위의 수식에서 $k \rightarrow \infty$ 일 때, $v_k$ 는 $v_{\pi}$로 수렴 (Converge) 하고, 이를 통해 Policy에 대한 가치 함수를 추정할 수 있다. 구현 관점에서 실제로 무한번을 반복할 수 없으므로, 임의의 작은 값 $\theta$ 에 대해, $| v_{k+1}(s) - v_{k}(s) | < \theta$ 를 만족하면 Policy Evaluation을 위한 반복을 중단한다.
- 2-1-3. Policy Improvement
Policy Evaluation을 통해 가치 함수를 구했다면, 모든 State에 대해 기존의 Policy (Old Policy)를 다음과 같이 Greedy Policy를 통하여 업데이트한다.
\[\pi(s) \leftarrow \arg \max_{a} \sum_{s', r} p(s', r | s, a) \left\{ r + \gamma v_k(s') \right\}\]만약, Old Policy와 Greedy Policy가 동일하다면 기존의 Policy와 State-Value Function을 Optimal Policy와 Optimal State-Value Function으로 리턴한다. Old Policy와 Greedy Policy가 동일하지 않다면 업데이트된 Policy를 이용하여 Policy Evaluation-Policy Improvement 과정을 Old Policy와 Greedy Policy가 동일해질 때 까지, 반복 수행한다.
- 2-1-4. Pseudo Code
Policy Iteration 알고리즘을 Pseudo Code로 나타내면 다음과 같다.
Policy Iteration Algorithm Pseudo Code
2-2. Value Iteration
Policy Iteration 알고리즘에서는 먼저 모든 state에 대해 policy evaluation을 통해, 가치함수를 계산하고 policy improvement를 수행하였다. Value Iteration 알고리즘은 Policy Iteration과 달리 every time step 마다 다음 수식을 통해, Policy Evaluation과 Policy Improvement를 동시에 수행한다.
\[v_{k+1}(s) \leftarrow \max_{a} \sum_{s', r} p(s', r | s, a) \left\{ r + \gamma v_k(s') \right\}\]위의 수식에서 $k \rightarrow \infty$ 일 때, 도출된 $v_k \thickapprox v_{*}$ 는 Optimal Value Function이고, 이 Value Function에 대해 Greedy Policy를 이용하여 Optimal Policy를 도출한다.
\[\pi(s) = \arg \max_{a} \sum_{s', r} p(s', r | s, a) \left\{ r + \gamma v_k(s') \right\}\]- Pseudo Code
Value Iteration 알고리즘을 Pseudo Code로 나타내면 다음과 같다.
Value Iteration Algorithm Pseudo Code
3. Conclusion
DP 알고리즘에서 Policy Iteration과 Value Iteration 모두 Optimal Policy의 수렴성을 보장하지만 알고리즘의 복잡도 측면에서 Policy Iteration이 Value Iteration 방법보다 효율이 좋은 것으로 알려져 있다.
모든 이론이 동일하지만 글로 내용을 이해하는 것보다 구현을 통해 이론을 적용해보면 훨씬 수월하게 개념을 이해할 수 있다. 다음 포스팅에서는 Python 기반의 프로그래밍을 통해, 4 X 4 Grid World 문제에 대해 DP를 적용하여 풀어가는 예제를 다룬다.