Dynamic Programming Example - Grid World

1. Introduction

본 포스팅에서는 Python 코드를 통해, Dynamic Programming (DP) 알고리즘을 구현하는 내용을 다룬다. 앞선 포스팅에서 다룬 Policy Iteration 알고리즘을 이용하여 4X 4 Grid World에 대한 Value Function과 Optimal Policy를 도출한다. 코드 구현을 위해 필요한 Python Package는 NumPy 이다.

2. MDP Environment

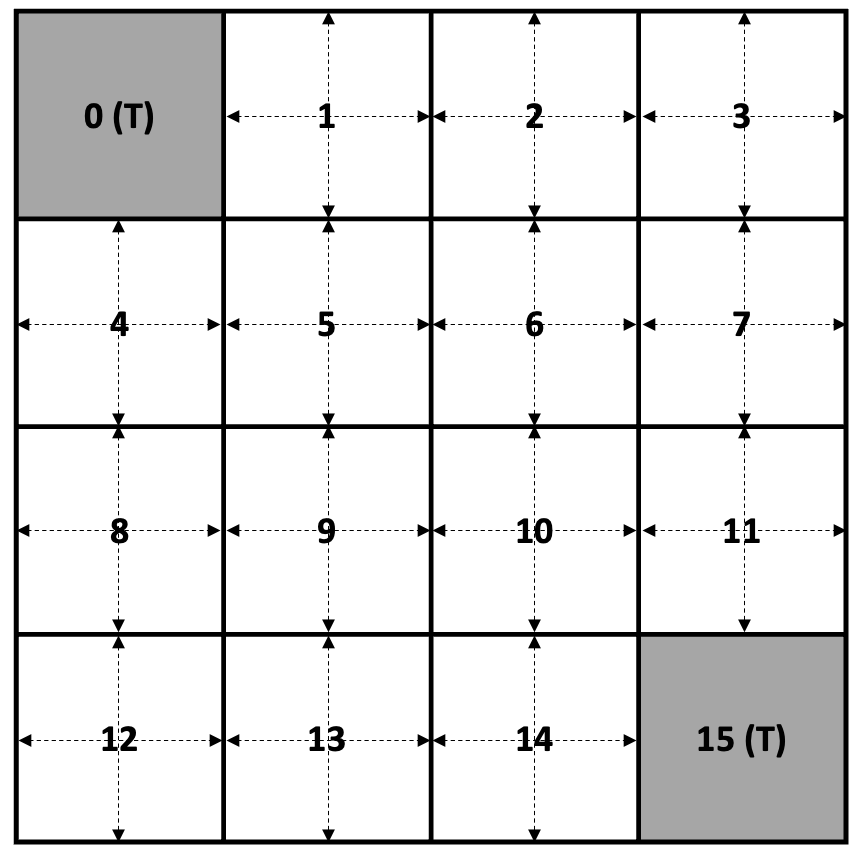
MDP 환경은 다음 그림과 같은 4 X 4 Grid World 이다.

4X4 Grid World

위의 Grid World에서 Agent의 목표는 각 State에서 Terminal State로 이동하는 최적의 Policy를 찾는 것이다.

2-1. State

총 0~15 까지 16개의 State가 있고, 0과 15는 Terminal State이다.

2-2. Action

Terminal State를 제외하고, 1~14의 State에서 다음과 같이 4가지 방향으로 이동하는 Action이 존재한다.

• 0: Move Left
• 1: Move Down
• 2: Move Rigth
• 3: Move Up

만약 Action을 취하였을 때 다음 State가 Grid를 벗어나는 경우에는 다음 State와 현재 State는 동일하다.

2-3. Reward

State에서 Action을 취하였을 때, 다음 State가 Terminal일 경우에는 Reward는 $0$ 이고, 그 이외의 경우에 대한 Reward는 모두 $-1$ 이다.

2-4. MDP Dynamics (State Transition Probability)

DP를 적용하기 위해서 Agent는 MDP의 Dynamics를 알고 있어야 한다. 4 X 4 Grid World에서는 취하는 Action에 따라 State Transition이 Deterministic 하다. 예를 들어, State 1 에서의 State-transition probability는 다음과 같다.

\[p(s'=0, r=0 | s=1, a=0) = 1\] \[p(s'=5, r=-1 | s=1, a=1) = 1\] \[p(s'=2, r=-1 | s=1, a=2) = 1\] \[p(s'=1, r=-1 | s=1, a=3) = 1\]

만약, Model-Free 환경일 경우에는 Agent는 Action에 따른 State Transition이 Non-Deterministic 하기 때문에 위와 같이 State Transition Probability로 표현할 수 없다. 예를 들면, 위의 예시에서 Model-Free 환경에서는 State 1에서 action 0을 취했을 경우에 다음 State가 반드시 0이라는 보장을 할 수 없고, 그 확률 또한 알 수 없다. Model-Free한 환경에 대한 알고리즘은 후술할 Monte Carlo 기법과 관련된 포스팅에서 더 자세히 다룬다.

3. Implementation

import numpy as np
import copy

'''
Dynamic Programming (Policy Iteration) for 4 X 4 Grid World

=====State Table=====

0(T) 1    2     3
4    5    6     7
8    9    10    11
12   13   14    15(T)

=====================

====Action===

0: Move left
1: Move down
2: Move right
3: Move up

=============
'''
class Grid_Env():
    def __init__(self, num_states, grid_width=4, grid_height=4, discount=0.9):
        super().__init__()
        self.num_states = num_states
        self.grid_width = grid_width
        self.grid_height = grid_height
        self.discount = discount

        self.terminal = [0, self.num_states - 1] # Terminal state

        self.num_actions = 4
        self.action_move = [(0, -1), (1, 0), (0, 1), (-1, 0)]  # left, down, right, up

        self.value_table = np.zeros([self.num_states], dtype=float)
        self.policy = np.zeros([self.num_states], dtype=int)

        self._initialize()

    def _initialize(self):
        self.value_table = np.random.uniform(0, 1, self.num_states)

        self.policy = np.random.randint(self.num_actions, size=self.num_states)
        self.policy[0] = -1
        self.policy[-1] = -1

        print("Initial value table: \n {}".format(self.value_table.reshape(self.grid_height, -1)))
        print("Initial policy: \n {}".format(self.policy.reshape(self.grid_height, -1)))

    def get_state(self, state, action):
        is_terminal = False

        state_row = state // self.grid_width
        state_col = state % self.grid_width

        next_state_row = state_row + self.action_move[action][0]
        next_state_col = state_col + self.action_move[action][1]

        if next_state_row < 0:
            next_state_row = 0
        elif next_state_row > self.grid_height - 1:
            next_state_row = self.grid_height - 1

        if next_state_col < 0:
            next_state_col = 0
        elif next_state_col > self.grid_width - 1:
            next_state_col = self.grid_width - 1

        next_state = next_state_row * self.grid_width + next_state_col

        if next_state in self.terminal:
            is_terminal = True

        if is_terminal:
            reward = 0
        else:
            reward = -1

        return next_state, reward, is_terminal

    def cal_action_value(self, state):
        action_value = np.array([0, 0, 0, 0], dtype=float)
        for act in range(self.num_actions):  # left, right, up, down
            next_state, _, _ = self.get_state(state, act)
            action_value[act] = self.value_table[next_state]

        return action_value

    def policy_evaluation(self):
        value_table_mem = copy.deepcopy(self.value_table)
        iter_cnt = 0

        # Policy iteration until value table converges (small delta)
        while True:
            iter_cnt = iter_cnt + 1

            for state in range(self.num_states):
                if state not in self.terminal:
                    next_state, reward, is_terminal = self.get_state(state, self.policy[state].item())
                    value = reward + self.discount * self.value_table[next_state]
                    value_table_mem[state] = round(value, 3)

            delta = np.linalg.norm(self.value_table - value_table_mem)
            self.value_table = copy.deepcopy(value_table_mem)  # Update value table memory

            if delta < 0.1:
                print("Iteration for value table: {}, Value Table: \n {}, \n delta: {:.2f}"
                      .format(iter_cnt, self.value_table.reshape(self.grid_height, -1), delta))
                break


    def policy_improvement(self):
        stable = True

        for state in range(self.num_states):
            if state not in self.terminal:
                old_policy = self.policy[state]
                action_value = self.cal_action_value(state)
                greedy_action = np.argmax(action_value)

                # If greedy action is different from the old policy, policy is not stable
                if greedy_action != old_policy:
                    stable = False
                    self.policy[state] = greedy_action  # Policy update (improvement)

        if stable:
            print("Policy is optimal")

        return stable

    def policy_mapping(self):
        policy_map = np.empty([self.num_states, 1], dtype=str)

        for state in range(self.num_states):
            if state not in self.terminal:
                if self.policy[state] == 0:
                    policy_map[state] = 'L'
                elif self.policy[state] == 1:
                    policy_map[state] = 'D'
                elif self.policy[state] == 2:
                    policy_map[state] = 'R'
                elif self.policy[state] == 3:
                    policy_map[state] = 'U'
            else:
                policy_map[state] = 'T'

        return policy_map.reshape(self.grid_height, -1)

def run_dp():
    env = Grid_Env(num_states=16)
    iter_cnt = 0

    while True:
        iter_cnt = iter_cnt + 1
        env.policy_evaluation()
        is_stable = env.policy_improvement()

        print("Policy iteration: {}, Value Table: \n {}".format(iter_cnt, env.value_table.reshape(4, -1)))
        print("Policy iteration: {}, Policy: \n {}".format(iter_cnt, env.policy.reshape(4, -1)))

        if is_stable:
            policy_map = env.policy_mapping()
            print("Final Policy: \n {}".format(policy_map))
            break

    return env

if __name__ == "__main__":
    env = run_dp()

3-1. 코드 설명

Grid_Env 클래스를 정의하고, inital policy와 inital value table을 초기화 한다. Grid_Env 클래스의 주요 method 목록은 다음과 같다.

• get_state()

현재 state와 action을 받아 다음 state와 reward, terminal state indicator를 리턴한다.

• policy_evaluation()

현재 policy에 대한 무한 loop를 통해서 value table을 계산하여 update 한다. 이전에 계산된 value table과 현재의 value_table 계산 결과를 비교하여 충분히 작은 값일 경우, 무한 loop를 종료한다.

• policy_improvement()

Value table 결과를 바탕으로 모든 state에서 greedy action 기반으로 policy를 update 한다. Policy Update를 모두 수행한 이후, environment의 policy에 대한 stable 여부를 리턴한다. (Old Policy == Greedy Policy 일 경우에만 True 리턴)

3-2. 코드 실행 결과

초기화된 initial policy와 initial value table에 따라 소요되는 policy iteration 횟수에 차이가 있으나 대략 3~4번의 policy iteration으로 optimal policy에 수렴한다. 각 State에서 도출되는 optimal policy는 다음과 같다.

Final Policy: 
 [['T' 'L' 'L' 'L']
 ['U' 'L' 'L' 'D']
 ['U' 'L' 'D' 'D']
 ['U' 'R' 'R' 'T']]

Optimal Policy 결과를 확인하면 직관적으로 Terminal State 에 가장 빨리 도달할 수 있는 Action을 취하는 것을 확인할 수 있으며, 일부 State에 대해서는 Multiple Action이 Optimal Policy가 될 수 있지만 편의상 L > D > R > U 순으로 Action에 대한 우선 순위를 두어 1개의 Action만 취하도록 하였다.

4. Conclusion

본 포스팅에서는 Policy Iteration 에 대한 Pseudo Code를 간단한 Grid World 환경에 대한 Example을 통해 Python을 이용하여 구현하였다. DP는 Agent가 Model을 정확히 알고 있어야 적용할 수 있다는 한계가 있고, 실제로 접하게 되는 대다수의 RL 문제에서는 MDP의 Dynamics를 알지 못한다. MDP의 Dynamics를 알지 못하는 경우 DP를 적용하지 못하더라도 DP에서 사용한 개념은 Model-Free한 MDP를 풀기 위한 토대가 된다. 다음 포스팅 부터는 Model Free 한 환경에서 MDP를 풀기 위한 방법에 대해 다룬다.