Monte Carlo Method
1. Introduction
Dynamic Programming (DP)는 Bellman Eq.를 풀기 위해 Model의 Dynamics, 다시 말하면, MDP의 State transition Probabilty 를 알고 있어야 적용이 가능한 방법이다 (Model-based). 그러나 대부분 접하게되는 MDP 문제에서는 State Transition Probability를 정확하게 알 수 없다.
현재까지는 State와 Action이 모두 Discrete한 domain의 경우만 다루었지만 State 또는 Action이 Continuous한 domain의 경우에는 당연히 State Transition Probabilty를 알 수 없다. 뿐만 아니라, State와 Action이 모두 Discrete한 domain의 경우에도 바둑이나 블랙잭 처럼 State와 Action의 복잡도에 따라 Dynamics를 사실상 알 수 없는 경우가 존재한다.
간단한 예시로 앞선 포스팅에서 DP의 예시인 다루었던 Grid World에서 Dynamics를 추가한 MDP를 생각해보자. Grid World에서는 Action (상,하,좌,우) 에 따라 다음 State가 Action의 방향으로 이동하도록 Discrete하게 고정되었는데 $(1)$ Action 대로 움직이지 않을 확률이 존재하여 Action을 수행한 이후의 다음 State가 무엇인지 특정할 수 없는 경우, $(2)$ State에도 랜덤성이 있어 Action에 따라 어떤 방향으로 이동할 경우 1칸 보다 많이 이동할 확률이 존재하여 다음 State가 무엇인지 특정할 수 없는 경우가 발생한다면 State별 Action에 따라 고려해야 하는 state transition이 무수히 많아질 것이다.
단순하게 Action과 State에 랜덤성이 추가되는 것만으로도 Model의 Dynamics가 매우 복잡해지게 되는 것이다. Action에만 랜덤성을 대표적인 MDP의 예시는 OpenAI Gym에서 제공하는 Frozen Lake의 사례가 있다. Frozen Lake는 목표는 Grid World와 유사하게 시작점에서 Hole에 빠지지 않고 도착지점 까지 도착하는 것이고, 미끄러짐 옵션 (is_slippery=True)을 주게 되면 반드시 Action으로 선택한 방향대로 움직이는 것이 아니라 확률에 따라 다른 방향으로 움직일 확률이 존재한다.
이와 같이 Agent가 MDP의 Dyanmics를 모르더라도 (Model-Free) Bellman Eq.를 풀기위한 알고리즘 중 하나가 Monte-Carlo (MC) 방법 이다. MC 부터가 본격적인 강화학습 문제를 푸는 시작점이라고 할 수 있다.
2. MC Algorithm
MC도 DP와 유사하게 MDP에서 Policy를 평가 (Policy Evaluation) 하고, Policy를 개선 (Policy Improvement) 하는 Policy Control 하는 과정을 수행한다. MC는 Algorithm은 Model의 Dyanmics를 모르는 경우에 MDP를 풀기 위해 무수히 많은 Sampling의 과정을 거친다.
MC에서 Policy Evaluation을 위한 가장 기본적인 원리는 일단 어떤 Policy에 따라 Agent가 MDP의 환경에서 시작점부터 종료가될 때까지 Action을 수행을 하고 역으로 가치함수를 도출해 나가는 것이다. Agent가 시작점에서 종료될 때 까지 Policy에 따라 정책을 수행하는 일련의 과정을 Episode라 한다. 즉, MC는 무수히 많은 Episode를 Sampling하면서 가치함수를 업데이트 해나가는 알고리즘이라 할 수 있다.
Sampling을 통해 Value Function을 구하는 과정은 마치 주사위 2개를 굴렸을 때 나오는 눈의 합의 기대값을 도출하기 위해 반복 시행을 통해 나온 값을 평균을 구하는 원리와 유사하다고 할 수 있다. 즉, 우리는 이미 2개의 주사위를 구렸을 때 눈의 합의 기대값이 7이라는 것을 알고 있지만, 실제로 주사위 2개를 굴린 이후 눈의 합을 구하는 과정 (Episode) 을 반복 수행한 이후, 평균을 낸 값도 Episode의 개수가 많아질 수록 큰 수의 법칙에 의해 7에 근사한 값이 나오는 원리와 동일하다.
2-1. Action-Value Function (Q-function) in MC
DP에서는 가치 함수으로 State-Value Function을 사용하였다. 하지만 MC에서는 가치 함수로 Action-Value Function (Q-function)을 주로 사용한다. DP에서는 Model을 알고 있기 때문에 State-Value Function이 있으면 최적 Policy를 도출할 수 있지만, Model을 모르는 경우에는 State-Value Function 자체만으로는 최적 Policy를 결정할 수 없기 때문이다. 즉, Agent가 state transition probabilty를 알고 있다면 State-Value Function을 통해, 최적의 State를 향해 나아가는 Action을 결정할 수 있지만 Agent가 state transition probability를 알 수 없다면 State-Value Function 만으로 최적의 State를 향해 나아가는 Action을 결정할 수 없다. 따라서, MC를 포함하여 Model-free한 환경에서는 State별 수행가능한 모든 Action에 대한 Q-function을 가치함수로 사용한다.
2-2. MC Policy Control
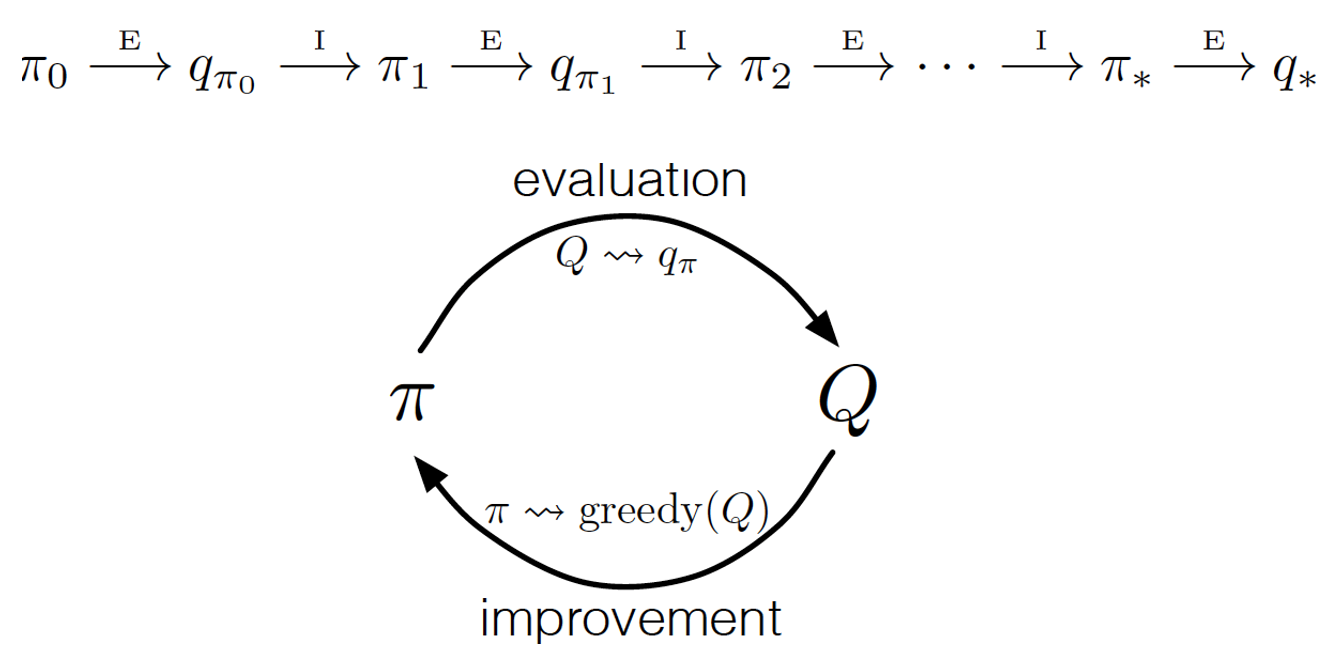
MC에서는 가치함수로 Q-function을 사용한다는 점을 제외하고, MC에서의 Policy Control은 DP에서 Policy Control과 매우 유사하다.다음과 같이 MC Control에서는 Policy에 따라 Q-function을 평가 (Evaluation) 하고, Greedy Policy에 의해 Policy를 업데이트 (Improvement) 한다.
Policy Control을 할 때, State-Action Pair가 중복되는 경우, 가장 첫번째 State-Action Pair만 이용할 것인지 (first-visit) 모든 State-Action Pair를 이용할 것인지 (every-control)에 따라 알고리즘에 차이가 있으나 두 방법 모두 Policy가 수렴한다고 알려져 있고 본 포스팅에서는 first-visit control을 다룬다.
- Initialization
MDP 환경에 대해 임의의 Policy ($\pi_{0}$)로 초기화 하고, 모든 State에 대하여 Q-function ($q_0(s, a)$)을 임의의 값으로 초기화 한다.
- MC Control
- Episode Generation
시작 State부터 종료 State까지 Policy를 따르는 Episode를 다음과 같이 생성한다.
\[\pi: S_0, A_0, R_1, ..., S_{T-1}, A_{T-1}, R_{T}\]생성된 Episode에 따라 Terminal State 부터 역순으로 time step을 돌면서 누적 Reward를 계산한다.
\[G_t = R_{t+1} + \gamma G_{t+1}\]- Policy Evaluation
특정 Time-step $t$에서의 State-Action Pair $(S_t, A_t)$ 가 해당 Episode의 $0 \sim (t-1)$ 까지의 time-step에서 발생하지 않았을 경우 (first-visit), 현재까지 Episode에서 구해진 Q-function $Q(S_t, A_t)$과 평균을 취하여 값을 업데이트 한다.
실제 알고리즘을 구현하는 경우에는 평균을 취하지 않고 다음과 같은 수식을 통해 업데이트 한다.
\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (G - Q(S_t, A_t))\]여기서 $\alpha$ 는 머신러닝 알고리즘에서 모델을 업데이트하는 정도를 의미하는 학습률 (learning rate)이다. 위와 같은 수식의 유도과정은 Incremental Implementation 참고하자.
- Policy Improvement
$Q(S_t, A_t)$ 를 업데이트한 이후, 다음과 같이 $S_t$ 에서의 Greedy Action을 구한다.
\[A^{*} = \arg \max_{a} Q(S_t, a)\]Greedy Action을 구한 이후, 다음 수식에 따라 $\forall a \in A(S_t)$에 대해, $S_t$ 에서의 policy를 Update 한다. (Epsilon-Greedy)
\[\pi(a|S_t) \leftarrow \left\{ \begin{array} {rcl}{1 - \epsilon + \frac{\epsilon}{|A(S_t)|}} & \mbox{for } a=A^{*} \\ \frac{\epsilon}{|A(S_t)|} & \mbox{for } a \neq A^{*} \end{array} \right\}\]
2-3. Pseudo Code
MC Control 알고리즘을 Pseudo Code로 나타내면 다음과 같다.
 MC Control Algorithm Pseudo Code
MC Control Algorithm Pseudo Code
3. Incremental Implementation
어떤 State-Action Pair에 대해, 누적 보상값의 평균은 다음과 같이 주어진다.
\[Q(S, A) = \frac{1}{N(S, A)} \sum_{i=1}^{N(S, A)}G_{i}(S, A)\]편의상 State와 Action에 대한 symbol을 제거하고, 위 수식을 다시 쓰면 다음과 같이 표현할 수 있다.
\[Q_{N+1} = \frac{1}{N} \sum_{i=1}^{N}G_{i}\]위의 수식을 전개하여 풀어쓰면 다음과 같이 나타낼 수 있다.
\[Q_{N+1} = \frac{1}{N} \left( G_N + \sum_{i=1}^{N-1}G_i \right) = \frac{1}{N} \left[ G_N + (N-1)\frac{1}{(N-1)}\sum_{i=1}^{N-1}G_i \right]\] \[= \frac{1}{N} \left[G_N + (N-1)Q_N \right] = Q_{N} + \frac{1}{N}(G_N - Q_N)\]따라서 $ \frac{1}{N} \leftarrow \alpha $ 로 치환하면 위의 수식은 다음과 같이 표현된다.
\[Q_{N+1} = Q_{N} + \alpha(G_N - Q_N)\]4. Conclusion
DP가 Model을 알고 있는 환경에서 Value Function을 계산 (Compute)하는 알고리즘이라면 MC는 Model을 모르고 있는 환경에서 Sampling을 통해 Value Function을 학습 (Learn)하는 알고리즘이라고 볼 수 있다. MC Control은 하나의 Episode가 온전히 종료되어야만 Q-function을 업데이트할 수 있다는 한계가 있고, 이와 같은 한계를 극복하기 위해 Time-Difference (TD) 기법이 도입되었다. MC에서 사용한 개념은 DQN에 이르기 까지 Model-Free한 환경에서 강화학습 문제를 다루기 위한 토대가 된다. 다음 포스팅에서는 Python 기반으로 Frozen Lake 환경에서 MC를 구현하는 예제를 다룬다.