Monte Carlo Method Example - Frozen Lake

1. Introduction

본 포스팅에서는 Python 코드를 통해, Monte Carlo (MC) Method 알고리즘을 구현하는 내용을 다룬다. 앞선 포스팅에서 다룬 MC Control Algorithm을 이용하여 OpenAI Gym의 Frozen Lake 환경에 대한 Value Function과 Optimal Policy를 도출한다. 코드 구현을 위해 필요한 Python Package는 Gym, Numpy, Matplotlib 이다.

2. MDP Environment

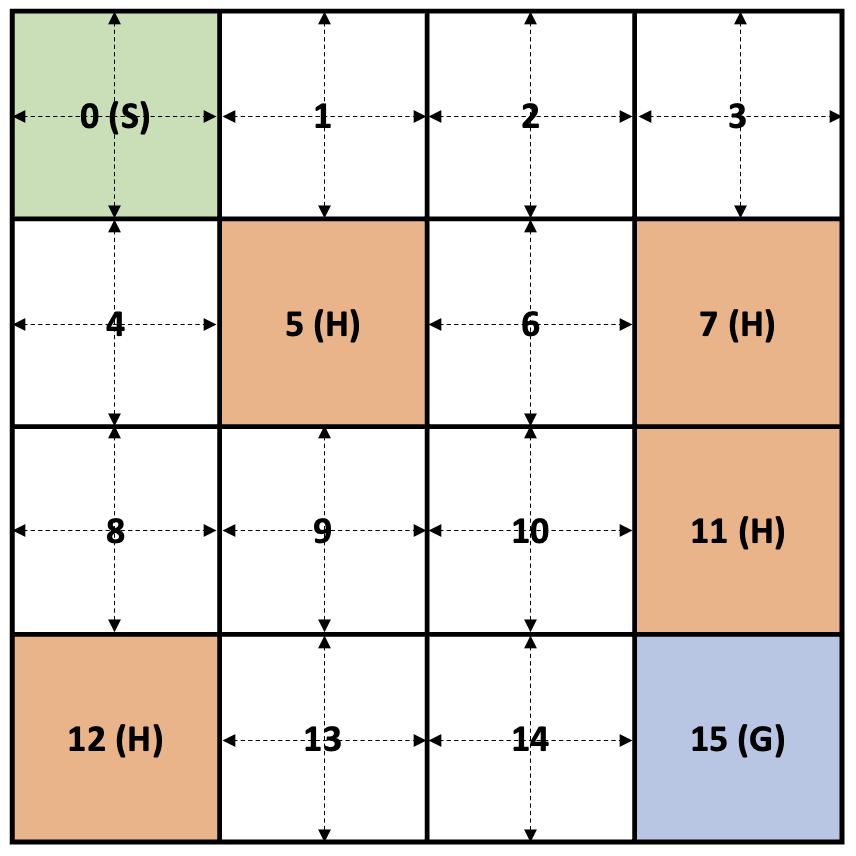
Frozen Lake의 MDP 환경은 다음과 같은 4X4 Grid World와 유사하며, 총 16개의 Grid 중 4개는 Hole이 있는 형태이다.

Frozen Lake

위와 같은 MDP 환경에서 Agent의 목표는 Hole에 빠지지 않고, 시작 지점부터 목표 지점까지 가는 것이다.

2-1. State

총 0~15 까지 16개의 State가 있고, State 0은 시작점, State 5, 7, 11, 12는 Hole, State 15는 Goal 이다. 여기서 Goal과 Hole은 Terminal State로 Agent가 Terminal State에 도달하면 Episode가 종료된다.

2-2. Action

Terminal State를 제외한 11개의 State에서 다음과 같이 4가지 방향으로 이동하는 Action이 존재한다.

• 0: Move Left
• 1: Move Down
• 2: Move Rigth
• 3: Move Up

만약 Action을 취하였을 때 Next_State가 Grid를 벗어나는 경우에는 Next_State와 현재 State는 동일하다.

2-3. Reward

State에서 Action을 취하였을 때, Next_State가 Terminal이 아닐 경우에는 Reward는 $0$ 이고, Next_State가 Terminal 일 경우 Terminal이 Hole일 경우의 Reward는 $0$ 이고, Terminal이 Goal일 경우의 Reward는 $1$ 이다.

• 위의 Reward는 Default 환경에서의 값이고, 구현 과정에서 커스터마이징이 가능하다.
• 실제 구현 과정에서는 Next_State가 Terminal이고, Terminal이 Hole일 경우의 Reward를 $-1$로 설정하였다.

2-4. MDP Dynamics (State Transition Probability)

DP 예시에서의 Grid World와 달리 Frozen Lake에서는 is_slippery=True일 경우, Action에 따른 State transition이 다음과 같이 Non-deterministic 하다.

• Agent가 어떠한 Action을 선택하여 행동을 취하더라도 실제 이동하는 방향은 선택한 Action의 반대 방향을 제외하고 모두 $1/3$의 확률을 갖는다.
• 예를 들면, is_slippery=True일 경우, State 9에서 Action이 0 (Move left)일 경우, State Transition Probability는 다음과 같다.

\[p(s'=8, r=0 | s=9, a=0) = \frac{1}{3}\] \[p(s'=5, r=-1 | s=9, a=0) = \frac{1}{3}\] \[p(s'=13, r=0 | s=9, a=0) = \frac{1}{3}\]

2-5. Why use Action-Value Function (Q-function)?

Frozen Lake의 경우 비교적 단순한 환경이므로 각 State에서 State Transition Probability를 통해 State-Value Function을 구할 수 있다. 그러나 특정 State에 대해서 Action에 따라 State Transition이 결정되는 것이 아니라 확률에 따라 State Transition이 결정되기 때문에 State-Value Function을 통한 Optimal Policy를 도출할 수 없다. (Model-Free) 따라서, 각 State에서 행동 가능한 Action에 대한 가치를 판단하는 Q-function을 통해 Optimal Policy를 도출한다.

3. Implementation

import gym
import numpy as np
import copy
import random
import matplotlib.pyplot as plt

'''

SFFF
FHFH
FFFH
HFFG

action
0: Left
1: Down
2: Right
3: Up

'''

class MC_Agent:
    def __init__(self, env, discount=0.9, learning_rate=0.01):
        super().__init__()
        self.env = env
        self.num_states = env.observation_space.n
        self.num_actions = env.action_space.n
        self.state_goal = self.num_states - 1 # 15
        self.state_terminal = list([5, 7, 11, 12, self.state_goal]) # Hole + Goal

        self.discount = discount
        self.learning_rate = learning_rate

        self.action_value_table = np.zeros([self.num_states, self.num_actions], dtype=float)
        self.policy = np.zeros([self.num_states, 1], dtype=int) # Except terminal state policy

        self._initialize()

    def _initialize(self):
        self.action_value_table = np.random.uniform(0, 1, (self.num_states, self.num_actions))
        self.action_value_table[self.state_terminal] = 0

        self.policy = np.random.randint(self.num_actions, size=(self.num_states, 1))
        self.policy[self.state_terminal] = -1

        print("Initial action-value table: \n {}".format(self.action_value_table))
        print("Initial policy: \n {}".format(self.policy.reshape(4, -1)))

    def gen_episode(self):
        state_memory = [0]
        action_memory = []
        reward_memory = []

        state = self.env.reset()
        action = random.randint(0, self.num_actions - 1) # Exploring action at initial state

        done = False
        success = False

        while not done:
            action_memory.append(action)
            state, reward, done, _ = self.env.step(action)

            if done:
                if state != self.state_goal:
                    reward = -1
                else:
                    success = True
                    reward = 1
            else:
                reward = 0.0
                state_memory.append(state)

            reward_memory.append(reward)
            action = self.policy[state].item()


        memory = list(zip(state_memory, action_memory, reward_memory))

        return memory, success

    def policy_control(self, memory, epsilon):
        memory_copy = copy.deepcopy(memory)
        memory_copy.reverse()
        state_action_memory = [ (mem[0], mem[1]) for mem in memory_copy ]

        reward_agg = 0
        for step in reversed(memory):
            state_action_memory.pop(0)
            state, action, reward = step
            reward_agg = self.discount * reward_agg + reward

            if (state, action) not in state_action_memory:
                q_val = self.action_value_table[state][action]
                self.action_value_table[state][action] = q_val + self.learning_rate * (reward_agg - q_val)
                greedy_action = np.argmax(self.action_value_table[state])

                coin = random.random()
                if coin < epsilon:
                    self.policy[state] = random.randint(0, self.num_actions - 1)
                else:
                    self.policy[state] = greedy_action

    def set_greedy_policy(self):
        for state in range(self.num_states):
            greedy_action = np.argmax(self.action_value_table[state])
            self.policy[state] = greedy_action
        self.policy[self.state_terminal] = -1

    def policy_mapping(self):
        policy_map = np.empty([self.num_states, 1], dtype=str)

        for s in range(self.num_states):
            if self.policy[s] == 0:
                policy_map[s] = 'L'
            elif self.policy[s] == 1:
                policy_map[s] = 'D'
            elif self.policy[s] == 2:
                policy_map[s] = 'R'
            elif self.policy[s] == 3:
                policy_map[s] = 'U'
            else:
                policy_map[s] = 'T'

        return policy_map.reshape(4, -1)

def run_mc(num_episodes, num_verifications):
    env = gym.make('FrozenLake-v1', is_slippery=True)

    result_train = []
    result_test = []

    agent = MC_Agent(env, discount=0.9, learning_rate=0.01)

    for n_epi in range(num_verifications):
        _, success = agent.gen_episode()
        result_test.append(success)

    result_test = np.array(result_test)
    print("Initial accuracy: {:.3f}".format(result_test.sum()/num_verifications * 100))

    for n_epi in range(num_episodes):
        epsilon = max(0.01, 0.30 - 0.1 * (n_epi / 200))  # Linear annealing from 30% to 1%
        memory, success = agent.gen_episode()
        agent.policy_control(memory, epsilon)
        result_train.append(success)

    result_train = np.array(result_train)

    fig, ax = plt.subplots(1,1)
    ax.plot(result_train)
    ax.set_xlabel('Episode')
    ax.set_ylabel('Success')
    plt.pause(0.01)

    result_test = []
    agent.set_greedy_policy() # Setup Greedy Policy

    policy_map = agent.policy_mapping()
    print("Final Greedy Policy: \n {}".format(policy_map))

    for n_epi in range(num_verifications):
        _, success = agent.gen_episode()
        result_test.append(success)

    result_test = np.array(result_test)
    print("Accuracy after MC control: {:.3f}".format(result_test.sum()/num_verifications * 100))

    env.close()

    return agent

if __name__ == "__main__":
    agent = run_mc(num_episodes=15000, num_verifications=5000)

3-1. 코드 설명

Frozen Lake 환경에 dynamics를 주기 위해 is_slippery=True로 하여, gym 모듈을 사용하여 다음과 같은 MDP 환경을 만든다.

env = gym.make('FrozenLake-v1', is_slippery=True)

MC Control Algorithm을 적용하기 위한 MC_Agent 클래스를 정의하고 initial policy와 Q-function을 초기화 한다. MC_Agent 클래스의 주요 method는 다음과 같다.

• get_episode()

Agent의 policy에 따라 State 0 부터 Action을 수행하여 episode가 종료될 때 까지의 모든 (State, Action, Reward)를 memory buffer에 저장한다. Episode가 종료되었을 때, Terminal state 가 Goal일 경우 success 변수에 True를 할당하고, 그렇지 않을 경우 False를 할당하여 memory buffer와 함께 리턴한다.

• policy_control()

MC Control Algorithm에 따라 memory buffer의 State, Action, Reward를 reverse time step으로 순회하며 Action-Value Function과 Policy를 업데이트 한다.

3-2. 코드 실행 결과

MC Control을 적용하기 전, initial policy 기반으로 Frozen Lake를 수행하면 Goal에 도달할 확률은 0에 가깝다. 총 15000의 Episode 동안, discount factor=0.9, learning rate=0.01로 설정한 이후, epsilon을 $30\% \rightarrow 1\%$로 감소시키면서 MC Control Algorithm을 적용하였다. Episode의 초반부에는 Goal에 도달하지 못하고 Hole에 빠지는 경우가 많지만, Episode가 진행될 수록 Goal에 도달하는 경우가 많아지며, 최종적으로 도출된 Greedy Policy는 다음과 같다.

Final Greedy Policy: 
 [['L' 'U' 'U' 'U']
 ['L' 'T' 'L' 'T']
 ['U' 'D' 'L' 'T']
 ['T' 'R' 'D' 'T']]

해당 Greedy Policy에 따라 Frozen Lake를 수행하면 70% 이상의 높은 확률로 Goal에 도달하는 것을 확인할 수 있다.

연산 환경에 따라 도달되는 Policy와 정확도에는 차이가 있을 수 있다.

4. Conclusion

본 포스팅에서는 Model-Free한 MDP 환경에서 MC Control 에 대한 Pseudo Code를 간단한 Frozen Lake 환경에 대한 Example을 통해 Python을 이용하여 구현하였다. MC Control은 Model-Free한 환경에서도 적용 가능하다는 특징이 있으나, 1개의 Episode가 반드시 종료되어야 Policy가 업데이트 될 수 있다는 한계가 있다. 이러한 이유 때문에 Frozen Lake의 예제에서도 MC Control 알고리즘을 적용하였을 때, Q-function이 제대로 학습되지 않을 경우, 정확도가 높지 않는 경우가 발생하기도 한다. 다음 포스팅에서는 이러한 MC Control의 한계를 개선하기 위한 Temporal-Difference (TD) 방식에 대해 다룬다.

5. Reference

Frozen Lake Description