DQN improvement - DDQN, DDDQN

1. Introduction

앞선 포스팅에서는 가장 baseline되는 DQN과 관련된 이론을 소개하고, Cartpole을 통한 예제를 적용하여 DQN을 구현하였다. Main network와 target network의 분리, replay buffer의 도입으로 DQN의 성능이 향상되었으나 학습 진행 과정에서 불안정성 또한 확인된다. 본 포스팅에서는 다음 2가지 방법을 통해 DQN 성능을 추가로 향상시키는 방법에 대해 기술한다.

• (1) Q-function 목적 함수 변형 [1]
• (2) DQN 구조 변형 [2]

(1)의 방법은 Double DQN (DDQN) 과 관련된 내용이며, (2)의 방법은 Dueling architecture 와 관련된 내용으로 DQN에 관심이 있는 사람이라면 익숙한 논문에 소개되었다. (1)의 방법과 (2)의 방법은 모두 2016년 Google에서 소개하였으며, 2가지 방법을 동시에 적용한 기법을 Dueling Double DQN (DDDQN)이라 한다.

2. Double DQN

Double DQN은 아래와 같은 기존 DQN의 target value의 수식을 수정하여 agent의 성능을 향상시킨다.

\[Y_{t}^{DQN} = R_{t+1} + \gamma \max_{a'}Q \left( S_{t+1}, a' | \theta^{-} \right)\]

위의 수식에서 $\max$ operator 가 Q-value를 over-estimation 하는 경향이 있기 때문에, 학습 과정에서 성능이 불안정해지는 원인이 된다. 이와 같은 문제점을 보완하기 위해 Double DQN (DDQN)이 도입되었고, DDQN에서는 target value를 아래와 같이 수정한다.

\[Y_{t}^{DDQN} = R_{t+1} + \gamma Q \left( S_{t+1}, \text{arg}\max_{a'} Q ( S_{t+1}, a'| \theta) | \theta^{-} \right)\]

위의 DDQN에서의 target value 수식을 보면 next state에서 agent가 취하는 next action은 main network의 greedy policy 기반으로 이루어지며, (next state-next action) pair에 대한 Q-value는 target network 기준으로 계산되는 것을 알 수 있다. 2번의 Q-value 연산이 이루어지므로 Double DQN 이라고 명명되며, 줄여서 DDQN이라 한다. 위와 같이 기존 DQN의 over-estimation 문제를 해결하는 것만으로도 동일한 DQN과 동일한 네트워크 구조를 갖는 모델을 사용하더라도 성능 향상이 이루어졌음을 [1]에서 보였다.

3. Dueling Architecture

Double DQN이 target value를 구하는 수식을 수정하였다면 Dueling architecture는 학습 모델의 구조를 변형하여 agent의 성능을 향상 시키는 방법이다. Dueling architecture에서는 state의 가치를 판단하는 (State-value function) Value network와 해당 state에서의 행동에 대한 가치를 판단하는 Advantage network로 분리한 이후, 하나로 통합하여 (aggregation) Q-function 값을 구한다. 이 때, value network의 출력은 스칼라이며 advantage network의 출력은 가능한 action 개수의 크기를 갖는 벡터이다. 개념적으로 Q-function과 value network, adavantage network 사이의 관계식은 다음과 같이 표현된다.

\[A(s, a) = Q(s, a) - V(s)\] \[Q(s, a) = V(s) + A(s, a)\]

위 수식의 정의를 풀어서 해석하면 $Q(s, a)$는 특정 state에서 action이 취해졌을 경우에 대한 가치를 판단한다면, $V(s)$는 해당 state가 얼마나 가치 있는지를 판단하고, $A(s, a)$는 특정 state에서 모든 action에 대한 상대적인 중요도를 측정한다고 볼 수 있다. 따라서, 이와 같이 advantage network를 추가함으로써 dueling architecture를 사용하면 오직 하나의 행동에 대한 결과를 바탕으로 가치를 업데이트하는 기존 DQN 학습 모델의 구조와 달리 선택되지 않은 행동들에 대한 상대적인 가치를 업데이트할 수 있다는 이점이 있다. 실제 구현 시에는 aggregation시 max 또는 mean을 적용하여 아래와 같이 Q-function을 구하도록 구현한다.

• Max aggregation을 사용하는 경우

\[Q(s, a | \theta, \alpha, \beta) = V(s| \theta, \beta) + \left( A(s, a| \theta, \alpha) - \max_{a' \in |\mathcal{A}|} A(s, a' | \theta, \alpha) \right)\]

• Mean aggregation을 사용하는 경우

\[Q(s, a | \theta, \alpha, \beta) = V(s| \theta, \beta) + \left( A(s, a| \theta, \alpha) - \frac{1}{| \mathcal{A} |} \sum_{a'} A(s, a' | \theta, \alpha) \right)\]

일반적으로 mean aggregation을 사용하였을 경우의 성능이 더 좋다고 알려져 있으며 아래 그림을 통해 일반적인 DQN과 Dueling architecture를 적용하였을 경우 학습 모델의 구조 차이를 알 수 있다.

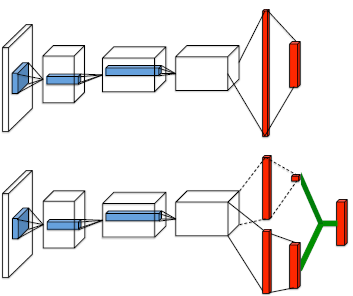Dueling architecture vs Vanilla DQN

한편, Dueling architecture는 target value를 구하는 수식과는 독립적이기 때문에 앞서 다룬 Double DQN과 결합하여 사용 가능하다. 따라서, Dueling architecture와 Double DQN을 결합한 구조를 Dueling Dobule DQN (DDDQN) 이라고 한다. DDDQN 구조를 적용하는 경우 Atari game에서 높은 성능 향상이 이루어졌음을 [2]에서 확인할 수 있다.

4. Conclusion

본 포스팅에서는 기본적인 DQN의 성능 향상을 위해, target 을 수정하는 DDQN, 학습 모델 구조를 수정하는 Dueling architecture에 대한 개념을 소개하였다. 다음 포스팅에서는 Cartpole 예제에 DDQN, DDDQN을 적용하여 DQN 대비 성능 개선이 어느정도 일어나는지 확인한다.

Reference

[1]

H. van Hasselt, A. Guez, and D. Silver, “Deep reinforcement learning with double Q-learning,” in Proc. 30th AAAI Conf. Artif. Intell. (AAAI), 2016, pp. 2094-2100.

[2]

Z. Wang et al., “Dueling network architectures for deep reinforcement learning,” in Proc. 33rd Int. Conf. Mach. Learn. (ICML), 2016, pp. 1995-2003.