Deep Q Network (DQN)

1. Introduction

TD Control Algorithm을 통해 Model-Free한 환경에서 매 time-step 마다 Agent가 Model을 업데이트하며 학습할 수 있는 것을 확인하였다. 그러나 앞서 살펴본 TD Control Algorithm에서는 모든 state와 action에 대한 Q-function (Q-table)을 구해야 한다는 한계가 있다. 따라서, TD Control Algorithm은 State와 Action이 모두 이산적 (Discrete)인 경우에만 적용 가능하다. 본 포스팅에서는 Action은 Discrete 하지만, State는 연속적 (Continuous)인 경우에 대해 적용할 수 있는 알고리즘인 Deep Q Network (DQN) 에 대해 다루고, Action까지 Continous한 경우에 대한 알고리즘은 차후 포스팅에서 다룬다.

DQN은 Q-learning과 기계학습에서 신경망 (Neural Network, NN)를 결합한 알고리즘으로 Q-function을 구하기 위해 신경망의 input으로 state를 사용한다는 점을 제외하고 Q-function을 구하는 수식 자체는 Q-learning과 동일하다. 본 포스팅에서는 강화학습을 공부하였다면 누구나 한번은 접해보았을 논문인 DQN 성능에 있어 놀라운 발전을 보여준 Nature에 개제된 논문 Human-level control through deep reinforcement learning에서 다룬 DQN 알고리즘과 그 원리에 대해 다룬다. DQN에서는 학습의 효율 개선을 위한 다음 2가지 특징이 추가된 점이 Q-learning에서 가장 크게 달라졌다고 볼 수 있다.

• Target Network
• Replay Buffer

2. DQN Algorithm

2-1. Continuous State Background

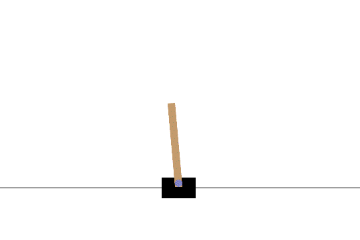
TD example 포스팅에서 다뤘던 Frozen Lake는 총 16개의 이산적인 State로 구성되어 있고, 문제를 풀기 위해, Terminal을 제외한 State에서 행동 가능한 Action의 조합에 따른 Q-table을 도출하였다. 그러나 Frozen Lake와 같이 State가 Discrete하지 않고, Continuous하거나 혹은 State의 개수가 Discrete 하더라도 그 개수가 매우 많을 경우, Q-table을 이용한 방법은 적용이 불가능하거나 Table에 대한 메모리가 State에 비례하여 기하급수적으로 증가하고, 모든 State에 대한 Q-table을 구하기 위한 시간 또한 크게 증가한다. Continuous한 State에 대한 예시로 DQN 구현 예제에서도 다룰 다음과 같은 Cartpole 환경을 생각해보자.

Cartpole

Cartpole 환경에 대한 구체적인 정보는 향후 예시에서 다룰 포스팅과 OpenAI gym 페이지를 참고하고, 본 포스팅에서는 State와 Action에 대해서만 간략하게 소개한다. Cartpole 환경에서 State는 다음과 같은 총 4개의 성분으로 구성된다.

• 카트의 위치 (Cart position): $-4 \sim 4$
• 카트의 속도 (Cart velocity): $-\infty \sim \infty$
• 폴의 각도 (Pole angle[radian]): $-0.418 \sim 0.418$
• 폴의 각속도 (Pole angular velocity): $-\infty \sim \infty$

반면, Cartpole 환경에서 Action은 Discrete한 2개의 Action (0: Move left, 1: Move right)으로만 구성된다.

위와 같은 Continuous한 성분으로 구성된 State에 대해서는 Q-table 방식을 적용할 수 없다. 이를 해결하기 위해, 기계학습에서 널리 사용되고 있는 심층 신경망 (Deep Neural Network, DNN) 구조가 도입되었다. DQN을 구현할 때, 아래와 같이 입력과 출력의 차원 (dimension)만 MDP 환경에 맞게 설정하면 DNN의 hidden layer 구조는 자유롭게 설정 가능하다.

• DQN 입력 차원: DQN의 입력 차원은 state의 차원과 동일하다.
• DQN 출력 차원: DQN의 출력 차원은 MDP의 Action Space 개수와 동일하다.

DQN의 입출력 차원의 원리에 대한 대한 개념은 다음 절에서 더 자세히 설명한다.

위의 Cartpole 예제에서 State를 구성하는 4개의 성분을 입력 차원으로 사용한다면 DQN 입력 차원은 $1 \times 4$의 vector가 되며, 출력 차원은 $1 \times 2$의 vector가 된다. Cartpole 예제에서 state를 4개의 성분으로 구성된 vector로 사용하지 않고, 관찰한 시점에서의 ($3 \times W \times H$) 차원의 RGB 이미지를 state로 구성한다면 DQN의 입력 차원 또한 ($3 \times W \times H$) 크기의 데이터를 입력으로 받는 Convolutional Neural Network (CNN)의 구조와 동일해진다. (이 경우에도 출력 차원은 동일하다.) 따라서, state가 더 복잡한 Matrix 형태, Cubic 형태로 구성된다면 DQN의 입력 또한 state의 차원과 동일하게 Matrix 형태, Cubic 형태로 구성하면 된다.

2-2. Action-Value function (Q-function) in DQN

이전 포스팅에서 다룬 Q-table에서는 관찰한 state에서 취한 action에 대한 state-action pair (Q-value)에 대한 값을 업데이트 하였다. DQN의 경우에는 관찰한 state를 설계한 NN 모델에 입력값으로 넣은 출력 결과를 Q-value 값으로 사용한다. 앞선 절에서 언급하였듯이 DQN의 출력 차원은 Action space의 크기와 동일한 이유는 이는 각각의 결과가 관찰한 state에 대한 Q-value를 의미하기 때문이다. 즉, continuous state의 경우에는 학습 과정에서 모든 state를 관찰할 수 없더라도 충분히 다양한 state에 대해 DQN 모델이 학습되었다면 학습 과정에서 경험하지 못했던 state가 입력으로 들어오더라도 정확한 결과를 도출해낼 수 있다. 결국, continuous state 또한 무수히 많은 discrete state의 집합이기 때문에 다양한 discrete state를 경험하며 DQN이 학습되었다면 마치 supervised learning의 원리와 같이 경험해보지 못한 state에 대해서도 높은 정확도를 보이게 되는 것이다.

여기까지 설명한 DQN의 입출력 차원을 왜 state의 차원과 action space의 크기로 정의하는지 그 원리를 이해하였다면 (원리를 정화히 이해하지 못하더라도), DQN 모델을 정의하여 학습을 시키면 어느정도 reasonable한 결과를 얻을 수 있을 것이다. 여기서 DQN의 성능을 더욱 향상시키기 위한 알고리즘으로 [1]에서 다음과 같은 Target Network와 Replay Buffer 개념이 도입되었다.

• 2-2-1. Target Network

앞선 Q-learning 포스팅에서 다루었던 Q-function을 업데이트하는 수식은 다음과 같다.

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \max_{a'}Q(S_{t+1}, a') - Q(S_t, A_t) \right]\]

본 포스팅의 서론에서 소개하였듯이 DQN에서도 Q-learning과 마찬가지로 Q-Network를 업데이트하기 위해 동일한 수식을 사용한다. 위의 수식에서 알 수 있듯이, 최종적인 학습을 하기 위한 Loss function은 다음과 같다.

\[L = R_{t+1} + \gamma \max_{a'}Q(S_{t+1}, a') - Q(S_t, A_t)\]

1개의 Q-Network만 사용할 경우, 위의 수식에서 Q-Network를 업데이트하기 위해 $S_{t+1}$ 에서의 Q-value를 구할 때 사용하는 Q-Network ($\max_{a’}Q(S_{t+1}, a’$) 또한 학습 단계마다 업데이트되는 것을 알 수 있다. 따라서, 원래 목표로 하던 $Q(S_t, A_t)$를 업데이트가 다른 $S_{t+1}$ 에서의 Q-value에도 영향을 미쳐 학습이 불안정해지는 문제가 있다. 이를 해결하기 위해 Target Network라는 별도의 Q-Network를 추가로 두었고, 일정 학습 단계마다 텀을 두어 Target Network를 업데이트 하도록 하였다. 즉, 원하는 Q-Network를 구성하는 파라미터를 $\theta$라 할 때, Target Network를 구성하는 파라미터를 $\theta^{-}$라 하면 Loss function은 다음과 같이 나타낼 수 있다.

\[L = R_{t+1} + \gamma \max_{a'}Q(S_{t+1}, a' | \theta^{-}) - Q(S_t, A_t | \theta)\]

Target network가 학습 network를 계속 추적할 수 있도록, $\theta^{-}$는 일정 학습 단계 주기에 따라 업데이트 시켜준다. 가장 단순한 업데이트 방법은 $\theta^{-}$를 $\theta$로 치환시키는 방법이고, 경우에 따라 업데이트 속도를 조절하기 위해 일부만 $\theta$를 추적할 수 있도록 하는 soft update 방식을 사용하기도 한다.

• 2-2-2. Replay Buffer

학습의 불안정성 문제를 해결하기 위해, Target Network를 도입하였지만 이것만으로는 충분하지 않다. DQN 또한 TD 방식으로 동작하는 알고리즘이므로 만약 time-step마다 Q-Network를 업데이트한다면 $S_t$에서의 경험과 $S_{t+1}$에서의 경험은 서로 밀접하게 연관되어 있어 업데이트가 불안정해질 수 있다. 따라서 이를 해결하기 위해 매 time-step마다 학습하는 것이 아니라 Replay buffer (혹은 Experience memory)를 두어, ($S_t$, $A_t$, $R_{t+1}$, $S_{t+1}$) set을 저장해둔 이후 buffer에 일정 크기 이상의 경험이 축적되었을 경우에만 정해진 batch size 만큼 Replay buffer에서 임의로 추출하여 학습을 진행하도록 한다.

Replay buffer는 FIFO (First-In-First-Out)의 큐 (Queue) 형태의 자료구조를 갖는 buffer로 설정한 buffer 크기 이상의 경험이 들어온 경우, 가장 오래된 경험을 폐기하고 가장 최신 경험을 저장한다.

• 2-2-3. Pseudo Code 본 포스팅에서 다룬 전체 DQN 알고리즘을 Pseudo code로 나타내면 다음과 같다. (출처: [1])

DQN Algorithm Pseudo Code

3. Reference

[1]

V. Mnih, K. Kavukcuoglu, D. Silver et al., “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533, 2015.